Change in Velocity
When I write the Greek letter Δ (delta) in front of a variable, I am talking about the change in that variable, usually between some initial moment and some final moment. For instance, $\Delta\vec v$ is the change in velocity, and $\Delta t$ is the change in time. The change in a variable A is defined aswhere $A_i$ is the variable's value at the initial moment and $A_f$ is its value at the final moment. The change in $A$ is also the value you need to add to the initial value to get the final value:
The change in a vector quantity, like velocity, works exactly the same way: $$\Delta\vec v=\vec v_f-\vec v_i=\vec v_f+(-\vec v_i)$$
Column
Consider this motion diagram.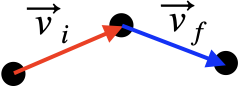
Column
To calculate the change in velocity, we take the negative of $\vec v_i$ and add it to $\vec v_f$, to get $\Delta \vec v$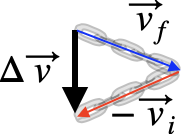
$${\color{blue}\vec v_f} + (-{\color{red}\vec v_i}) = \Delta v$$
Column
We can also think of $\Delta v$ as what we add to $\vec v_i$ to get $\vec v_f$: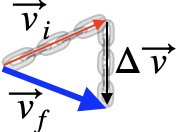
$${\color{blue}\vec v_f}={\color{red}\vec v_i}+\Delta \vec v$$
Note
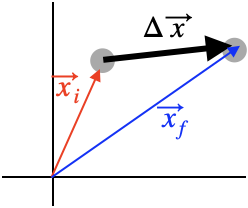
Remember that the displacement is written as $\Delta \vec x$? While it is easiest to think of it as the vector from one spot to another, we can think of it as a "change of position". To do that, we define the position vector of a spot as the vector from the origin to that spot.