Bernoulli's Equation
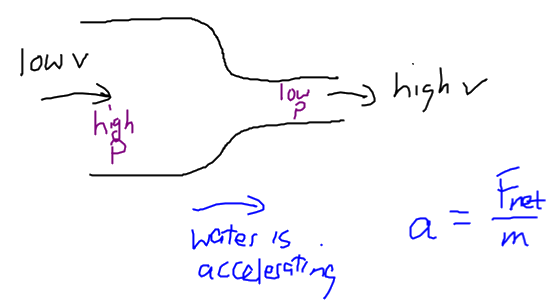
2) This means that the water is accelerating, and so there must be a net force to cause this acceleration.
3) This net force comes from the fact that the pressure decreases as the water speeds up.
In Flow Rate we said that when water moves from a wider to a narrower pipe, it speeds up: it accelerates. That must mean, according to Newton's Second Law, that there is a net force on the water pushing it from the wider end to the narrower end, and this force must come from the water itself. If the pressure in the water is higher where the pipe is wider, then the net force on the water will point to the right (in this figure) and we get the acceleration we need. This result can be generalized in a statement, known as Bernoulli's Principle:
We can express this in equation form by modifying our previous equation in How Pressure Varies with Depth to read
where $P_0$ is a constant of the fluid. In other words, moving fluid has $\frac12\rho_fv^2$ less pressure than it normally would.

For example, in a cup of still water, the speed is $v=0$ everywhere, and Bernoulli's equation becomes $P=P_{atm}+\rho_fgd$ as we found before. However, suppose we poke a hole into the side of the container, so that water can spill out. Just like the water at the surface, the water at the hole is also in contact with the open atmosphere, and so its pressure is also $P_{atm}$. This means that the added pressure $\rho_fgd$ due to the depth of the hole below the water's surface must be cancelled out by the pressure loss due to the flow of water. In other words: $$\rho_fgd=\frac12\rho_fv^2 \implies v=\sqrt{2gd}$$ The deeper the hole is below the surface, the faster the water will come out of the hole. As water runs out, however, $d$ becomes lower as the surface approaches the hole, and the speed drops: the water reduces to a trickle which stops when the surface reaches the hole.