3.
Static Equilibrium
When an object is not moving, the forces acting on that object must be balanced with each other. We say that such an object is in static equilibrium. That's so important, let me say that again:The forces on a stationary object must balance.

For example, a block with a weight of 50N sitting on a table is in static equilibrium because it is not moving. But we know it feels the force of gravity pulling it downward, so there must be another force pushing it upward to balance its weight. In this case, it is a normal force from the table which does so, and since the two forces must have the same strength, the normal force is also 50N.
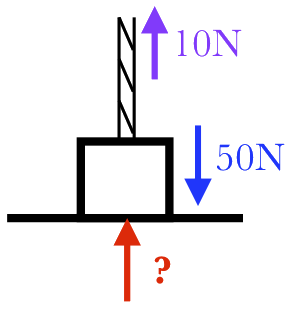
Suppose we attach a rope onto the same 50N block and pull it gently upward with a tension force of 10N. Now there are three forces acting on the block: tension and the normal force pointing up, and weight pointing down. If the forces balance, what must the normal force from the table be now? (Think about it before turning the page!)