Torque Problems

Calculating torque of a force $\vec F$

• Choose the pivot.
• Draw the lever arm $\vec r$ from the pivot to the point of contact. (Each force has its own lever arm: see (a).)

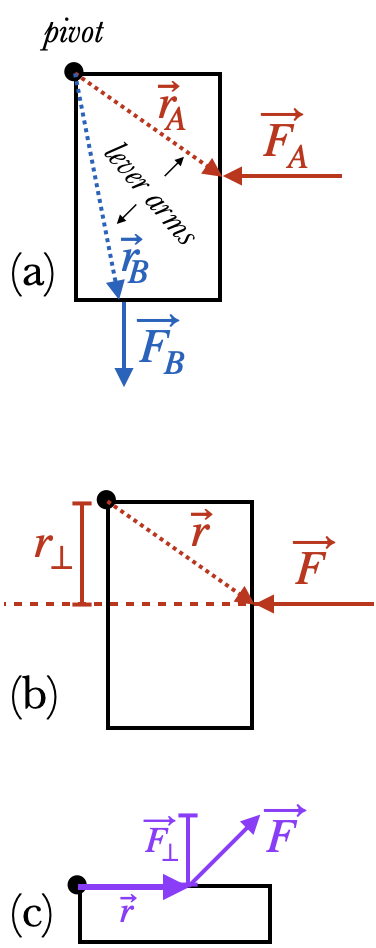
Consider special cases:

• if the force points directly at or away from the pivot, then the torque is zero
• if the force and lever arm are perpendicular to each other, then the torque is $\tau = rF$
• If you are given the angle $\theta$ between $\vec r$ and $\vec F$, then $\tau = rF\sin\theta$
• if the force is "level" (i.e. lies along an axis), draw a line through the force vector, and then measure the shortest distance from the pivot to that line. That is $r_{\perp}$, and the torque is $\tau = r_{\perp}F$ (See (b)).
• if the lever-arm is level, then find the component of the force $F_{\perp}$ that is perpendicular to the lever arm. Then torque is $\tau = rF_{\perp}$ (See (c)).
• Finally, add the sign:
• $+$ if the torque points counterclockwise around the pivot,
• $-$ if the torque points clockwise

Solving Torque Equilibrium Problems

• Draw a force diagram and create a force table. Add a column for torque.
• Fill out the force table's $x$ and $y$ columns as usual
• Don't forget any force from the pivot or hinge. (Call it a normal force.)
• Calculate the torque for each force.
• I recommend writing it as $(r)(F)$ rather than multiplying it out right away, to make it clearer what you're doing.
• Always include the sign.
• The torque column must add to zero as well.
• There will be three equations for three columns, so you can solve for three unknowns.